Συμπλήρωση τετραγώνου της αx² + βx + γ
Δυναμικό Φύλλο Εργασίας

Να απαντήσετε στις παρακάτω δραστηριότητες στο φύλλο εργασίας που θα κατεβάσετε από εδώ.

Δραστηριότητα 1 

Σέρνοντας την κόκκινη κορυφή περιστρέψτε το ορθογώνιο (2 φορές) ώστε να δημιουργηθεί τετράγωνο πλευράς

Ποιο είναι το εμβαδόν του αρχικού ορθογωνίου ως αλγεβρική έκφραση των x, b;

Ποιο είναι το νέο εμβαδόν του τετραγώνου; Να συγκρίνετε τις παραπάνω εκφράσεις. Τι συμπεράσματα βγάζετε;

Δραστηριότητα 2

Στο δυναμικό φύλλο εργασίας να σχηματίσετε τη συνάρτηση y = x² - 2 x + 4 = (x-1)²+3 θέτοντας κατάλληλες τιμές στα h, k

1. Ποιες είναι οι τιμές των α,β,γ και ποιες οι τιμές των h, k στις οποίες καταλήξατε;
2. Ποια είναι η θέση της συνάρτησης σε σχέση με την y = x²
3. Ποια είναι η ελάχιστη τιμή της συνάρτησης και για ποια τιμή του x επιτυγχάνεται;
4. Πως μετατοπίζεται η κορυφή της παραβολής σε σχέση με τις τιμές των h, k;

Δραστηριότητα 3  

Μεταβείτε στην ιστοσελίδα :

Οπτικοποίηση Συμπλήρωσης Τετραγώνου

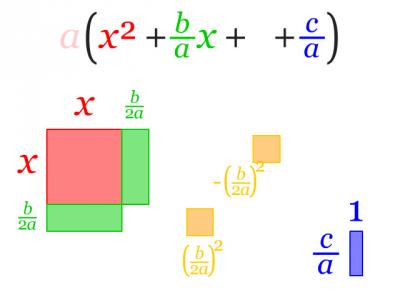
για να παρακολουθήστε την οπτικοποίηση όλης της απόδειξης της συμπλήρωσης τετραγώνου. Συζητήστε με τους συμμαθητές σας τις σας έκανε εντύπωση. Να καταγράψετε στο τετράδιό σας κάθε βήμα της απόδειξης διατυπώνοντας τον αλγεβρικό μετασχηματισμό και την γεωμετρική ερμηνεία του.

Δραστηριότητα 4 

1. Μετακινήστε τους δρομείς στις κατάλληλες θέσεις έτσι ώστε α = 1,  β = –4, γ = 5
2. Να βρείτε την κορυφή της παραβολής, την ελάχιστη τιμή της και τον άξονα συμμετρίας της. Περιγράψτε πως πρέπει να μετακινηθεί η παραβολή ώστε η κορυφή της να γίνει πάλι η αρχή των αξόνων και να συμπέσει πάνω στην y = x² .
3. Ποιες τιμές πρέπει να πάρουν οι παράμετροι α, β, γ έτσι ώστε η παραβολή να έχει κορυφή το σημείο Κ( 1, 1 );    
4. Με ποιες κινήσεις θα  μετατοπίσουμε τη γραφική παράσταση της  y=αx² , ώστε  να βρεθεί στη θέση της γραφικής παράστασης της y=αx² + βx +γ;

Πληροφορίες για τη Συμπλήρωση Τετραγώνου στην wikipedia